So, interesting outcome from the numbers - numbers don't lie, just people
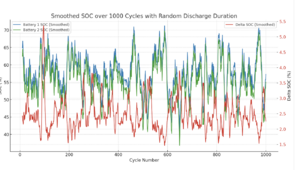
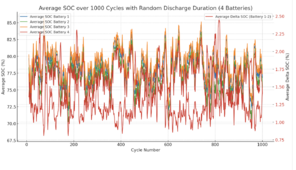
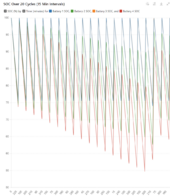
When the load interval is the same everytime the two batteries drift farther and farther apart until one bottoms out. When the load interval is random the batteries drift apart and back together again with no outside help.
I didn't expect this - So, the equalizer is a way to keep them closer together all the time, but if your usage pattern is random enough you don't actually need the equalizer.
View attachment 217816
I realize this is long - but please sanity check the work and let me know if you see anything I left out.
Once done I'll post the python code and details as a resource for seeing what an imbalance in strings of batteries or cells means.
Included are some graphs of how batteries drift apart and the raw calculations
If they stay together nice and tight that means the internal resistance of the batteries must be almost identical. This is not a given even from batteries that were next to each other on the assembly line.
Assume a charge voltage of 14.4v for a 12.8v battery, 28.8v for 24v battery, 58.4 for a 48v battery
I just measured a 12v LiTime battery at about 95% SOC and it is 2.05mΩ For battery #2 I am assumng 2.15 mΩ
OK, so I spent a few hours getting the AI to return good numbers that pass a sanity check
With a little AI help and giving it some constraints it spits out the deltas over time.
YES! - I know that AI suck at math - they are LLM not SPICE
that is usually when converting units and especially if you don't check the logic of the calcualtions.
And in all cases you have to sanity check all of the output and see if it is in the ballpark of what you expect.
And if it isn't what you expect double check every part of the math - sometime expectations are wrong
Where it gets tricky is the internal resistance varies with state of charge. This means the voltage at the end of a discharge cycle and charge cycle of each battery will be different on each.
Here are the constraints and formulas worked out
### Constraints:
1. **Two Batteries in Series**:
- Each is a LiFePO4 battery.
- Nominal battery voltage is 12.8V (25.6V for the series string).
2. **Initial SOC**:
- Both batteries start at 100% SOC.
3. **Discharge and Charge Parameters**:
- Usage (discharge) is fixed at 300 minutes.
- Battery 1 initial internal resistance: 2.05 mΩ.
- Battery 2 initial internal resistance: 2.15 mΩ.
- Charge voltage: 28.8V.
- Discharge current: 20A.
- Charge current: 50A.
- Discharge and charge cycles step through in 15-minute intervals.
4. **Resistance Based on SOC**:
- For Battery 1:
- SOC < 20%: 3.00 mΩ.
- SOC between 20% and 80%: 1.5 mΩ.
- SOC > 80%: 2.05 mΩ.
- For Battery 2:
- SOC < 20%: 3.15 mΩ.
- SOC between 20% and 80%: 1.65 mΩ.
- SOC > 80%: 2.15 mΩ.
5. **SOC Boundaries**:
- SOC cannot exceed 100%.
6. **Voltage Specifications**:
- Discharge Cutoff Voltage: 10V.
- Float Charge Voltage: 29.2V.
- Nominal Voltage: 25.6V.
- Maximum Voltage: 14.4V (per battery).
### Methods:
1. **Calculate Internal Resistance**:
- For Battery 1:
- \( \text{internal\_resistance} = \begin{cases}
0.00300 \text{ if SOC} < 20\% \\
0.00150 \text{ if SOC} \leq 80\% \\
0.00205 \text{ if SOC} > 80\%
\end{cases}
\)
- For Battery 2:
- \( \text{internal\_resistance} = \begin{cases}
0.00315 \text{ if SOC} < 20\% \\
0.00165 \text{ if SOC} \leq 80\% \\
0.00215 \text{ if SOC} > 80\%
\end{cases}
\)
2. **Calculate Voltage**:
- \( \text{voltage} = \max(10, \min(14.4, \text{nominal\_voltage} - (\text{current} \times \text{internal\_resistance}))) \)
3. **Calculate SOC from Voltage**:
- \( \text{SOC} = \frac{\text{voltage} + (\text{current} \times \text{internal\_resistance})}{\text{nominal\_voltage}} \)
4. **Discharge Phase**:
- Calculate SOC and voltage for each battery independently based on the discharge duration and internal resistance.
5. **Calculate Watts Used**:
- \( \text{Watts Used} = \text{voltage} \times \text{discharge current} \)
6. **Calculate Duration of Discharge**:
- Fixed at 300 minutes.
7. **Charge Phase**:
- Charge both batteries independently until one reaches 100% SOC.
- Stop charging when the first battery reaches 100% SOC, leaving the other battery slightly below 100%.
8. **Calculate Duration of Charge**:
- Calculated based on the difference between SOC at the end of discharge and the target SOC of 100%.
### Formulas:
1. **Internal Resistance Calculation**:
- For Battery 1:
- \( \text{internal\_resistance} = \begin{cases}
0.00300 \text{ if SOC} < 20\% \\
0.00150 \text{ if SOC} \leq 80\% \\
0.00205 \text{ if SOC} > 80\%
\end{cases}
\)
- For Battery 2:
- \( \text{internal\_resistance} = \begin{cases}
0.00315 \text{ if SOC} < 20\% \\
0.00165 \text{ if SOC} \leq 80\% \\
0.00215 \text{ if SOC} > 80\%
\end{cases}
\)
2. **Voltage Calculation**:
- \( \text{voltage} = \max(10, \min(14.4, \text{nominal\_voltage} - (\text{current} \times \text{internal\_resistance}))) \)
3. **SOC Calculation from Voltage**:
- \( \text{SOC} = \frac{\text{voltage} + (\text{current} \times \text{internal\_resistance})}{\text{nominal\_voltage}} \)
4. **Watts Used Calculation**:
- \( \text{Watts Used} = \text{voltage} \times \text{discharge current} \)
5. **Duration of Charge Calculation**:
- \( \text{Duration of Charge (min)} = \left( \frac{\text{capacity (Ah)} \times (\text{SOC\_end} - \text{SOC\_begin})}{\text{charge current}} \right) \times 60 \)
This setup ensures that the simulation accurately reflects the independent behavior of each battery during discharge and charge cycles, considering their specific internal resistances and SOC values. If further adjustments or additional analysis are needed, please let me know.
Here are resulting graphs
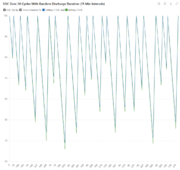
300 minute discharge cycle
discharge of 20 amps and charge of 50 amps.
First is SOC over 20 charge/dischage cycles in 15 minute intervals of charge discharge cycles
View attachment 217787
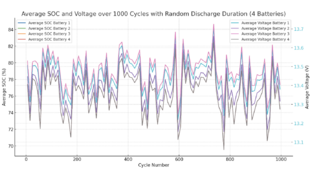
Voltage grap for both batteries over 20 charge/discharge cycles.
View attachment 217791
And here is a graph - 2 batteries - random cycle interval from 100 to 400 minutes. It would appear to mean that random cycles over time keep them in sync better than the same repeated cycle.
View attachment 217810